15.6.20

LaTeX en Blackboard con MathJax

Usando MathJax en Blackboard

Por: Darío Castro Castro

Matemáticas y texto

Acostumbrado a escribir en \LaTeX{} me era difícil adaptarme e escribir matemáticas usando el editor de ecuaciones de Blackboard y a la renderización que Blackboard hace de \LaTeX{}. Esto me llevó a leer muchas páginas web sobre escritura \LaTeX{} en páginas web. Históricamente, mostrar la notación matemática en los navegadores web ha sido un desafío. Afortunadamente las cosas han seguido adelante. En este post les presento las opciones disponibles para mostrar la notación matemática en el entorno de Blackboard que usamos en la Universidad. Un antecedente importante es que existe un compilador que pasa de \LaTeX{} a HTML: LaTeX2HTML. Sin embargo este es un proceso a veces engorroso en cualquier sistema operativo. Finalmente la búsqueda me llevó a tres soluciones:

  1. MathJax
  1. Markdown
  1. KaTeX

Les hablaré inicialmente de MathJax y de Markdown

LaTeX en Blackboard sin plugin

Blackboard permite introducir código \LaTeX directamente en la ventana de escritura. 

Soporte para notación matemática en Blackboard

Blackboard actualmente muestra notación matemática con Blackboard Math Editor. El editor de matemáticas está escrito por WIRIS, basado en estándares como MathML para representación interna y el formato de imagen PNG para mostrar fórmulas. La notación matemática se ingresa usando el editor gráfico de matemáticas y se muestra en un archivo de imagen.

Para la mayoría de las personas, Blackboard Math Editor es perfectamente adecuado. Sin embargo, para algunos temas y en algunos casos puede presentar problemas. Éstas incluyen:

  • Ya tiene una gran cantidad de notación escrita en un lenguaje de marcado matemático (es decir, \LaTeX), puede tomar mucho tiempo ingresar esto usando el editor gráfico de matemáticas en Blackboard.
  • Nativamente Blackboard muestra notación matemática en formato sans-serif. Para algunas áreas temáticas se prefiere una fuente serif.
  • Blackboard utiliza imágenes para mostrar la notación matemática, lo que puede generar problemas como: poca accesibilidad, imágenes borrosas y difíciles de leer al escalar, un ligero desenfoque de la notación cuando se imprime en papel, no hay opción para copiar y pegar la fórmula en otra aplicación para manipulación (por ejemplo, un sistema de álgebra computacional).
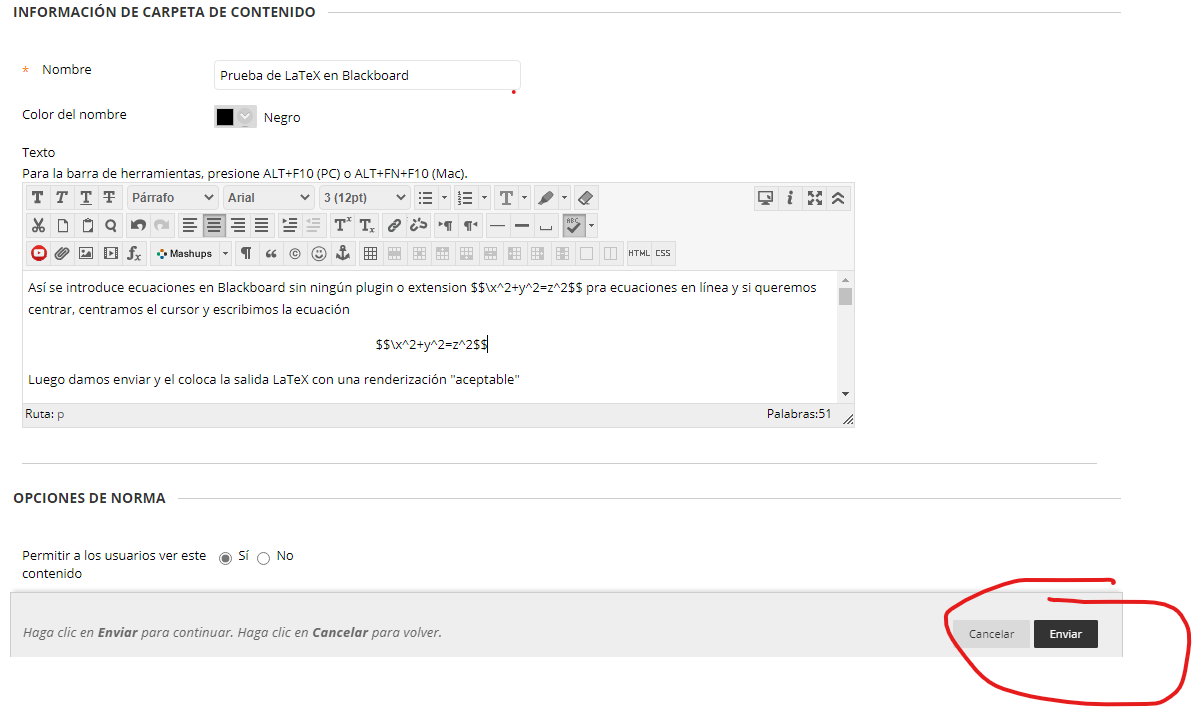
A continuación la forma de introducir ecuaciones en Blackboard sin ningún plugin o script externo

Así se introduce ecuaciones en Blackboard sin ningún plugin o extensión $$x^2+y^2$$ para ecuaciones en línea y si queremos centrar, centramos el cursor y escribimos la ecuación

$$x^2+y^2$$

Luego damos click en Enviar y el coloca la salida \LaTeX con una renderización "aceptable". El resultado se ve a continuación

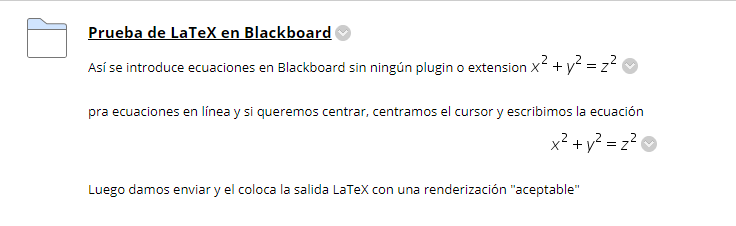
LaTeX en Blackboard con plugin: MathJax

Existen fundamentalmente dos plugins con diferentes configuraciones de \LaTeX que pueden ser incluidos en Blackboard

  • MathJax (y KaTeX)
  • Markdown

LaTeX en Blackboard con MathJax

MathJax es un motor de visualización de código abierto en JavaScript para la notación \LaTeX, MathML y ​​AsciiMath que funciona en todos los navegadores modernos (traducido de la documentación de MathJax). Su función es permitir la visualización de fórmulas matemáticas, sin importar su complejidad, a través de Internet y otros medios como el formato de libro electrónico ePUB.

MathJax proporciona tipografía de alta calidad y funciona en todos los navegadores modernos. La notación matemática es nítida y clara cuando se escala o imprime, y también se puede copiar y pegar en otras aplicaciones de software como Mathematica. Puede leer más sobre MathJax en

Mathematical notation on the web - part 1

Mathematical notation on the web - part 2

Usando MathJax en Blackboard

Puede usar MathJax en los siguientes tipos y herramientas de contenido de Blackboard:

artículos, carpetas, páginas en blanco, páginas de módulos, evaluaciones y encuestas, entradas de blog, entradas de wiki y entradas de glosario.

Usar MathJax en Blackboard es básicamente un caso de vinculación a la biblioteca en el código HTML del elemento de contenido y luego usar la notación \LaTeX estándar en el editor de texto (aunque el carácter delimitador difiere del utilizado en el marcado \LaTeX). Puede vincular directamente a la biblioteca MathJax en línea.

Existen muchas variaciones del plugin básico de Mathjax, pero después de mucho probar, encontré uno que sirviera con nuestra versión de Blackboard , encontré el apropiado

<script type="text/javascript"
   src="https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.7/MathJax.js?config=
   TeX-AMS_HTML,http://myserver.com/MathJax/config/local/local.js">
</script>

Se copia éste código antes de empezar es escribir y se pega en la ventana que se despliega en Blackboard al hacer clic en el botón HTML

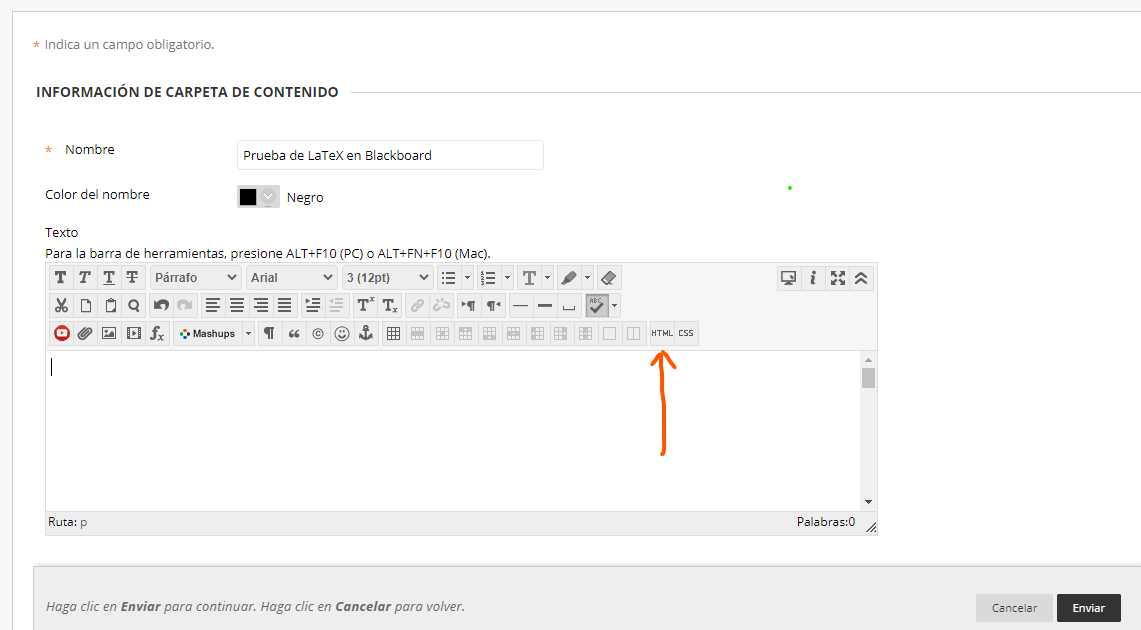
y nos debe quedar así:

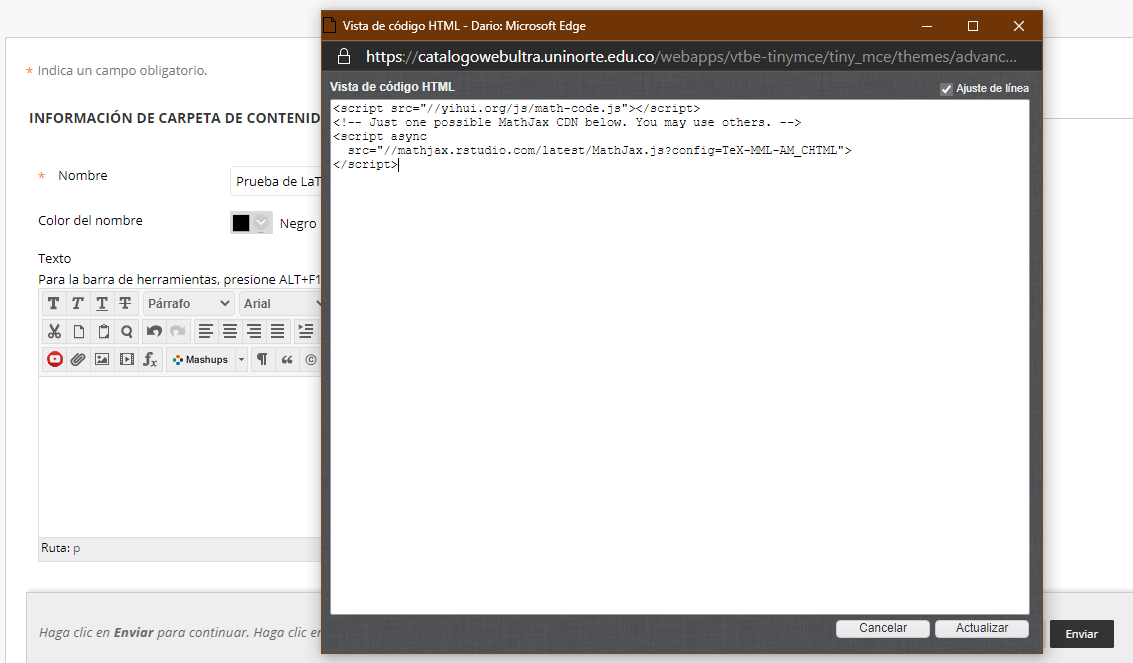
Le damos clic a actualizar y empezamos escribir directamente nuestro código \LaTeX.

Por defecto, el preprocesador MathJax define los delimitadores matemáticos LaTeX, que son \(...\)para matemática en línea y \[...\]para las ecuaciones mostradas. También define los delimitadores de TeX $$...$$para las ecuaciones mostradas, pero no define$...$como delimitadores matemáticos en línea. Esto se debe a que los signos de dólar aparecen con demasiada frecuencia en entornos no matemáticos, lo que podría ocasionar que algunos textos sean tratados como matemáticas de forma inesperada. Por ejemplo, con delimitadores de un solo dólar, "... el costo es de $ 2.50 por el primero, y $ 2.00 por cada uno adicional ..." causaría que la frase "2.50 por el primero, y" sea tratada como matemática ya que se encuentra entre signos de dólar.  Los comandos disponibles en MathJax los podemos encontrar en

http://www.onemathematicalcat.org/MathJaxDocumentation/TeXSyntax.htm


Los resultados serían estos

 

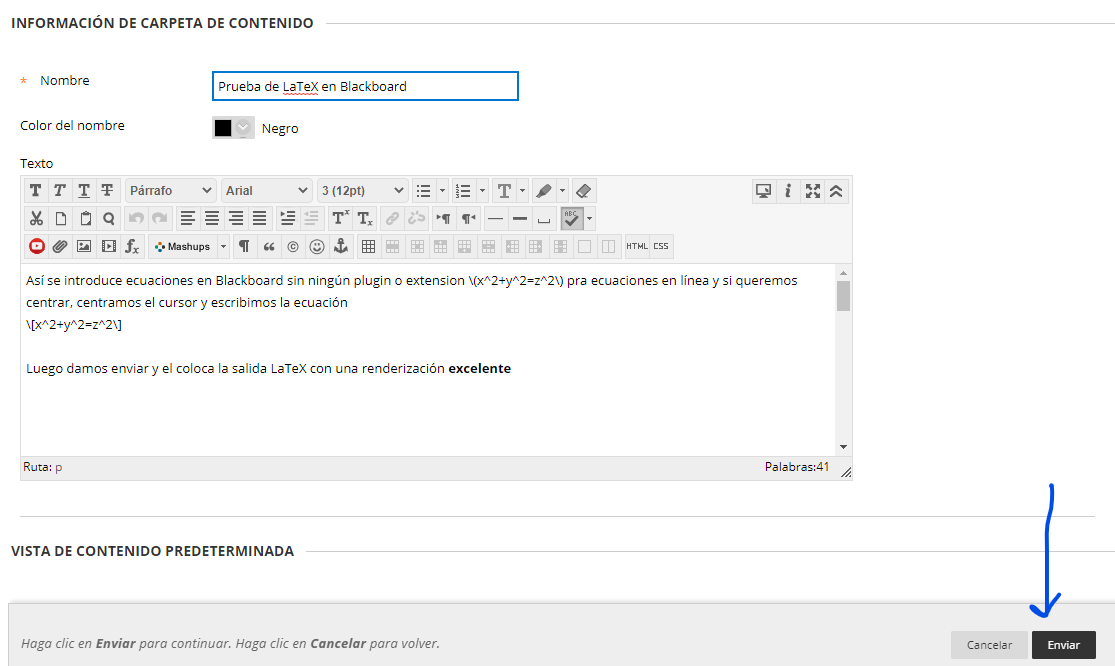
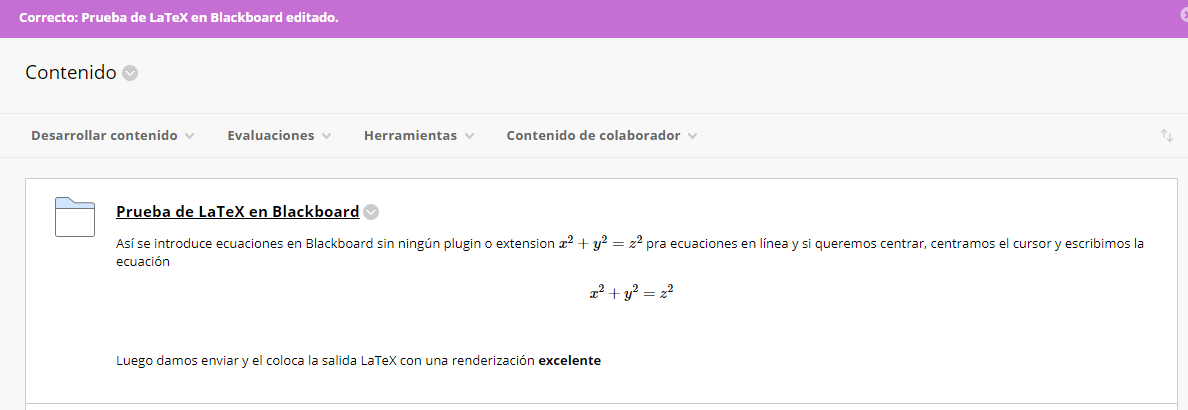
De esta manera podemos escribir código \LaTeX complejo y se compilará sin problemas. A continuación otros ejemplos:

 

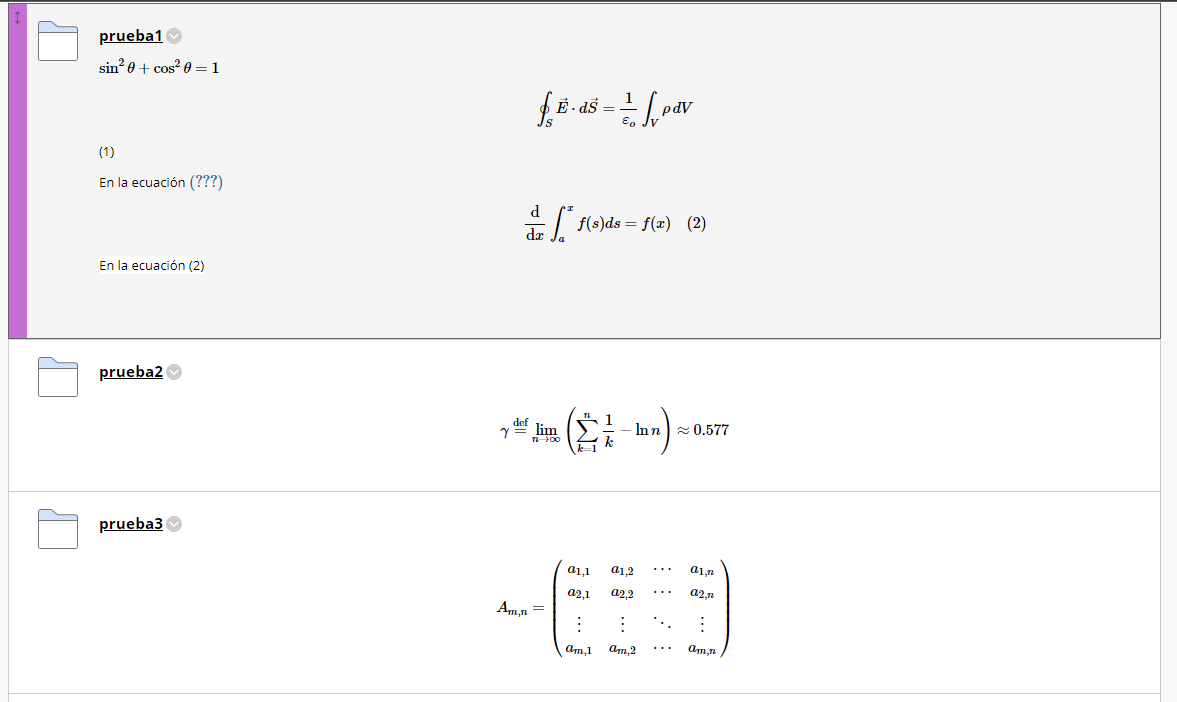
\LaTeX en Blackboard escribiendo en Markdown

Markdown es un lenguaje de marcado que facilita la aplicación de formato a un texto empleando una serie de caracteres de una forma especial. En principio, fue pensado para elaborar textos cuyo destino iba a ser la web con más rapidez y sencillez que si estuviésemos empleando directamente HTML. Y si bien ese suele ser el mejor uso que podemos darle, también podemos emplearlo para cualquier tipo de texto, independientemente de cual vaya a ser su destino.

Como explica "John Gruber": http://daringfireball.net/projects/markdown/, uno de sus creadores, Markdown es realmente dos cosas: por un lado, el lenguaje; por otro, una herramienta de software que convierte el lenguaje en HTML válido.

De Markdown existen variantes, unas soporta escritura \LaTeX otras no. Existen versiones instalables en el computador y existen versiones online. De las versiones online que estudié, la que mejor se adapta a nuestro propósito es

UPMATH

Aquí podemos escribir las ecuaciones como lo hacemos de costumbre en nuestro editor LaTeX, pero siempre escribiendo en código Markdown que no es nada difícil.

A continuación ejemplo cualquiera de código escrito en Markdown. Una vez se genera el código, copiamos el HTML que se genera y lo pegamos en Blackboard en la ventana HTML quedando un resultado así

Ejemplo de \LaTeX con Markdown

Let H be a Hilbert space, C be a closed bounded convex subset of H, T a nonexpansive self map of C. Suppose that as n\rightarrow\infty, a_{n,k}\rightarrow0 for each k, and \gamma_{n}=\sum_{k=0}^{\infty}\left( a_{n,k+1}-a_{n,k}\right) ^{+}\rightarrow0. Then for each x in C, A_{n}x=\sum_{k=0}^{\infty}a_{n,k}T^{k}x converges weakly to a fixed point of T .

The numbered equation

(1)u_{tt}-\Delta u+u^{5}+u\left| u\right| ^{p-2}=0\text{ in }\mathbf{R}% ^{3}\times\left[ 0,\infty\right[ \label{eqn1}%

is automatically numbered as equation (1)

(2)\boxed{ \int\limits_{-\infty}^{\infty} e^{-x^2} \, dx = \sqrt{\pi} }

(3)x_{1,2} = {-b\pm\sqrt{b^2 - 4ac} \over 2a}.

(4)A_{m,n} = \begin{pmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m,1} & a_{m,2} & \cdots & a_{m,n} \end{pmatrix}

(5)\[\oint_{S}\vec{E}\cdot d\vec{S}=\frac{1}{\varepsilon_o}\int_{V} \rho \, dV\]

(6)\gamma \overset{\text{def}}{=} \lim\limits_{n \to \infty} \left( \sum\limits_{k=1}^n {1 \over k} - \ln n \right) \approx 0.577

In this case the \LaTeX syntax will be highlighted in the source code. You can even add equation numbers (unfortunately there is no automatic numbering and refs support):

(7)|\vec{A}|=\sqrt{A_x^2 + A_y^2 + A_z^2}.

It is possible to write Cyrillic symbols in \text command: Q_\text{плавления}>0.

One can use matrices:

(8)T^{\mu\nu}=\begin{pmatrix} \varepsilon&0&0&0\\ 0&\varepsilon/3&0&0\\ 0&0&\varepsilon/3&0\\ 0&0&0&\varepsilon/3 \end{pmatrix},

integrals:

(9)P_\omega={n_\omega\over 2}\hbar\omega\,{1+R\over 1-v^2}\int\limits_{-1}^{1}dx\,(x-v)|x-v|,

cool tikz-pictures:

\usetikzlibrary{decorations.pathmorphing} \begin{tikzpicture}[line width=0.2mm,scale=1.0545]\small \tikzset{>=stealth} \tikzset{snake it/.style={->,semithick, decoration={snake,amplitude=.3mm,segment length=2.5mm,post length=0.9mm},decorate}} \def\h{3} \def\d{0.2} \def\ww{1.4} \def\w{1+\ww} \def\p{1.5} \def\r{0.7} \coordinate[label=below:$A_1$] (A1) at (\ww,\p); \coordinate[label=above:$B_1$] (B1) at (\ww,\p+\h); \coordinate[label=below:$A_2$] (A2) at (\w,\p); \coordinate[label=above:$B_2$] (B2) at (\w,\p+\h); \coordinate[label=left:$C$] (C1) at (0,0); \coordinate[label=left:$D$] (D) at (0,\h); \draw[fill=blue!14](A2)--(B2)-- ++(\d,0)-- ++(0,-\h)--cycle; \draw[gray,thin](C1)-- +(\w+\d,0); \draw[dashed,gray,fill=blue!5](A1)-- (B1)-- ++(\d,0)-- ++(0,-\h)-- cycle; \draw[dashed,line width=0.14mm](A1)--(C1)--(D)--(B1); \draw[snake it](C1)--(A2) node[pos=0.6,below] {$c\Delta t$}; \draw[->,semithick](\ww,\p+0.44*\h)-- +(\w-\ww,0) node[pos=0.6,above] {$v\Delta t$}; \draw[snake it](D)--(B2); \draw[thin](\r,0) arc (0:atan2(\p,\w):\r) node[midway,right,yshift=0.06cm] {$\theta$}; \draw[opacity=0](-0.40,-0.14)-- ++(0,5.06); \end{tikzpicture}

plots:

\begin{tikzpicture}[scale=1.0544]\small \begin{axis}[axis line style=gray, samples=120, width=9.0cm,height=6.4cm, xmin=-1.5, xmax=1.5, ymin=0, ymax=1.8, restrict y to domain=-0.2:2, ytick={1}, xtick={-1,1}, axis equal, axis x line=center, axis y line=center, xlabel=$x$,ylabel=$y$] \addplot[red,domain=-2:1,semithick]{exp(x)}; \addplot[black]{x+1}; \addplot[] coordinates {(1,1.5)} node{$y=x+1$}; \addplot[red] coordinates {(-1,0.6)} node{$y=e^x$}; \path (axis cs:0,0) node [anchor=north west,yshift=-0.07cm] {0}; \end{axis} \end{tikzpicture}

and the rest of LaTeX features.

Dario Castro, The LateX Expert!!
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)